Pythonのコードの書き方(セット)

今回はPythonの中でも重要なセットについて紹介します。

特徴

セットは重複を許さない集合を表現するときに使います。集合を表現できるため、集合演算をすることができます。また、リストやタプル、辞書など違って値に指定できるオブジェクトは変更できないものに限られます。それの特徴を以下のまとめました。

値の重複は許さない

セットは集合としてデータを扱うため、重複したデータを格納することはできません。重複したデータを格納した場合、エラーは発生せずにデータの登録がされません。

>>> a = set([１,2,3,2])
>>> a
set([１, 2, 3])

 

値には変更不可のオブジェクトのみ

以下のコードのように数値や文字列、タプルなどの変更不可なオブジェクトは値として格納することは出来ますが、辞書やリストのような変更可能なオブジェクトは値として格納することはできません。

>>> a = set([１,2,3])
>>> a
set([１, 2, 3])
>>> b = set([１,[2,3],4])
Traceback (most recent call last):
  File "", line 1, in 
TypeError: unhashable type: 'list'

 

2種類のセット

セットにはあとから変更可能なセット(set)とあとから変更不可能なセット(frozenset)があります。

>>> a = set([１,2,3])
>>> b = frozenset([１,2,3])
>>> a
set([１, 2, 3])
>>> b
frozenset([１, 2, 3])

 

集合演算ができる

セットは集合として表現できるため、集合同士の演算をすることができます。

>>> a = set([１,2,3])
>>> b = set([2,3,4])
>>> a.union(b)
set([１, 2, 3, 4])

 

セットを新しくつくる

冒頭でも紹介したようにセットにはオブジェクトの変更を許容するかによって作り方が変わります。

変更可能なセットをつくる(set(イテレータ))

変更可能なセットをつくるには『set([値1,値2,・・・])』を使います。イテレータはまた後日説明しますが、リストやタプルもイテレータに入ります。

>>> a = set([１,2,3])
>>> a
set([１, 2, 3])

変更不可能なセットをつくる(frozenset(イテレータ))

変更不可能なセットをつくるには『frozenset([値1,値2,・・・])』を使います。

>>> a = frozenset([１,2,3])
>>> a
frozenset([１, 2, 3])

 

セットの値を参照する

セットは値を集合として持ちます。そのため順次という概念がなく、リストやタプルのようにインデックスで指定ができません。また、辞書と違ってキーを持たないため、セットは通常の方法では値を参照できません。そのため、セットで値を参照するには「for文」を使って一つずつ値をセットから取り出します。ただし、順序の概念がないため、セットを定義した順序通りに値が取り出せる保証はないことに注意してください。

>>> a = set([１,2,3])
>>> for i in a:
...     print(i)
...
1
2
3

 

セットの値を更新する

セットにはインデックスの概念がないため、特定の値を変更することはできません。特定の値のみを更新するには後述する集合演算を使うか、一度対象の値を削除し、新たに値を追加する方法となります。ここでは、『.add(値)』を使って新たにセットに値を追加する方法を紹介します。なお、frozensetに対しては値を追加することはできません。

>>> a = set([１,2,3])
>>> a.add(4)
>>> a
set([１, 2, 3, 4])

 

セットの値を削除する

ここではセットの値の削除方法を４つ紹介します。なお、frozensetは値を削除することはできませんので、以下の方法は使うことはできません。

値を指定して削除する(.remove(値))

値を指定して削除する方法として『.remove(値)』があります。指定した値があれば、削除されますが、なければ「KeyError」が発生します。

>>> a = set([１,2,3])
>>> a.remove(3)
>>> a
set([１, 2])

 

値を指定して削除する(.discard(値))

もうひとつの値を指定して削除する方法として『.discard(値)』があります。これはremoveと比べて、指定した要素がセットになくてもエラーが発生しません。

>>> a = set([1,2,3])
>>> a.discard(3)
>>> a
set([1, 2])

 

値を一度取り出して削除する(.pop())

辞書にもあったように後続の処理のために、値を一度取り出してから削除するには『.pop()』を使います。ただし、何が取り出されるかは保証できません。取り出すものがない場合は「KeyError」が発生します。

>>> a = set([１,2,3])
>>> a.pop()
1

セット内の値を全て削除する(.clear())

セット内のすべての値を削除するには『.clear()』を使います。

>>> a = set([１,2,3])
>>> a.clear()
>>> a
set([])

 

集合演算の関数

セットは集合を表現できます。そのため、集合を使った演算式をいくつか列挙します。なお、集合演算を使うとセットの新規作成であったり、値の更新ができます。

論理和(集合A.union(集合B))

論理和とは各集合のそれぞれに含まれている値の総和です。このとき、共通で存在する値は一つとします。

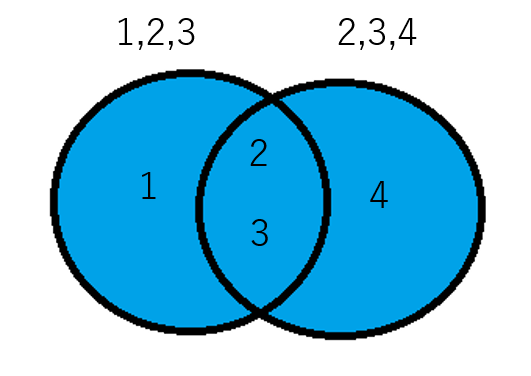
その集合の論理和を計算するには『集合A.union(集合B)』を使います。

>>> a = set([１,2,3])
>>> b = set([2,3,4]
>>> a.union(b)
set([１, 2, 3, 4])

 

論理積(集合A.intersection(集合B))

論理積とは集合Aと集合Bのそれぞれに共通する値の集合です。

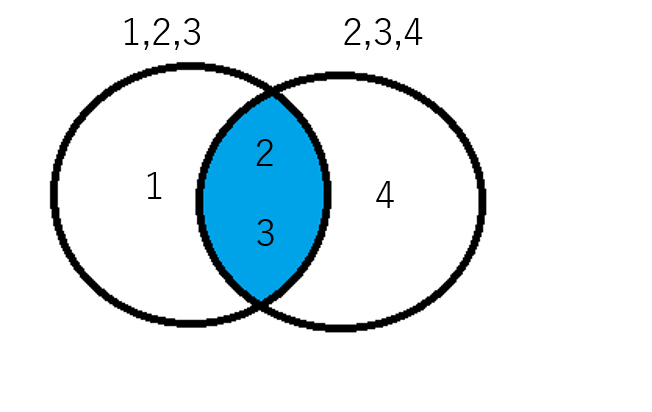
その集合の論理積は『集合A.intersection(集合B)』を使います。

>>> a = set([１,2,3])
>>> b = set([2,3,4])
>>> a.intersection(b)
set([2, 3])

 

差集合(集合A.difference(集合B))

差集合とは集合Aと集合Bを比べて、集合Bにない値の集合です。

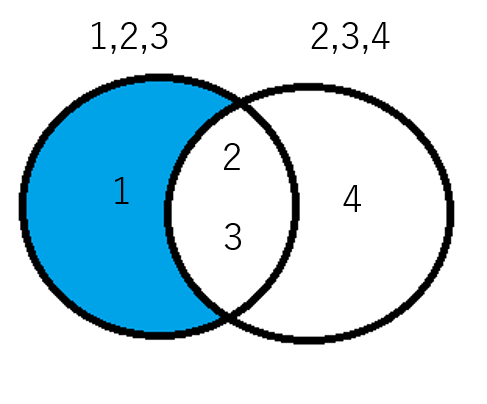
その差集合は『集合A.difference(集合B)』を使います。

>>> a = set([１,2,3])
>>> b = set([2,3,4])
>>> a.difference(b)
set([１])

 

対象差(集合A.symmetric_difference(集合B))

対象差とは集合Aと集合Bの共通でもっている値以外全てのことです。

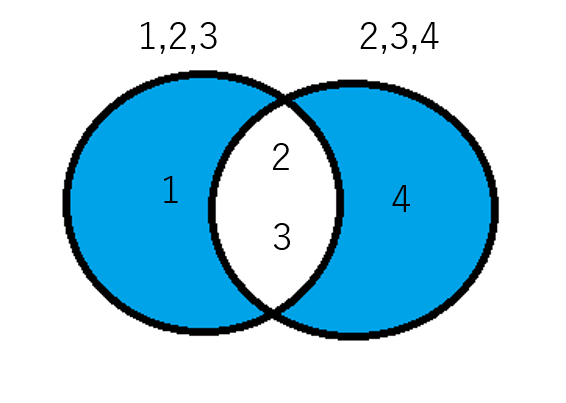
対象差は『集合A.symmetric_difference(集合B)』を使います。

>>> a = set([１,2,3])
>>> b = set([2,3,4])
>>> a.symmetric_difference(b)
set([１, 4])

 

集合演算子

今までは関数を使った演算をご紹介しましたが、演算子を使って直接演算をすることができます。ただし、両集合ともセット型である必要があります。

論理和	集合A | 集合B
論理積	集合A & 集合B
差集合	集合A – 集合B
対象差	集合A ^ 集合B

 

よくつかうもの

セットについてもよくつかうものを以下にまとめました。セットならではの関数などもあります。

部分集合の確認をする(集合A.issubset(集合B))

集合A内のすべての値が集合Bに含まれているかを確認します。確認するには『集合A.issubset(集合B)』を使います。全て含まれる場合は「True」、一つでも含まれないものがあれば「False」を返します。

>>> a = set([１,2,3])
>>> b = set([2,3,4])
>>> a.issubset(b)
False

 

上位集合の確認をする(集合A.issuperset(集合B))

これは部分集合の確認とは反対で、集合Bの全ての値が集合Aに含まれているかを確認します。確認するには『集合A.issuperset(集合B)』を使います。全て含まれる場合は「True」、一つでも含まれないものがあれば「False」を返します。

>>> a = set([１,2,3])
>>> b = set([2,3])
>>> a.issuperset(b)
True

 

指定した値がセットにあるかを調べる(値 in セット)

指定した値がセット内にあるかを調べるには『値 in セット』を使います。

>>> a = set([１,2,3])
>>> 2 in a
True

 

セット内の値の数を調べる(len(セット))

セット内の値の数を調べるには『len(セット)』を使います。

>>> a = set([１,2,3])
>>> len(a)
3

まとめ

以上。