パチンコ×統計学の可能性

日本には1000円で125玉を借りて、300分の1くらいで発生する大当たりを引く確率ギャンブル『パチンコ』という娯楽があります。
1日で10万円勝ったり、逆に10万円失ったりすることがあります。(私も昔はやっていました)
パチンコを統計学で見たときに勝率を上げることはできるのか。今回は統計学を別の角度から勉強していきたいなと思います。

正規分布

このブログでも過去に平均と標準偏差について触れてきました。今回はそれらを使った正規分布について説明したいと思います。

正規分布とは

正規分布とは最も身近にあるデータ分布です。そもそもデータ分布とは、観測されたデータが様々な値をとり、その在り方を表した様子です。観測したデータの在り方が全体で見たらどのような特徴があるのかがわかるとデータの予測や特徴が分かります。
正規分布は身近にあり、例えば人間の身長なんかも正規分布で表すことができます。

標準正規分布

正規分布の中でも基本的なモデルの標準正規分布を例に正規分布について説明します。

標準正規分布は平均値(μ)が0、標準偏差(σ)が1の正規分布です。0の値を中心に左右対称のため”標準”正規分布と呼ばれています。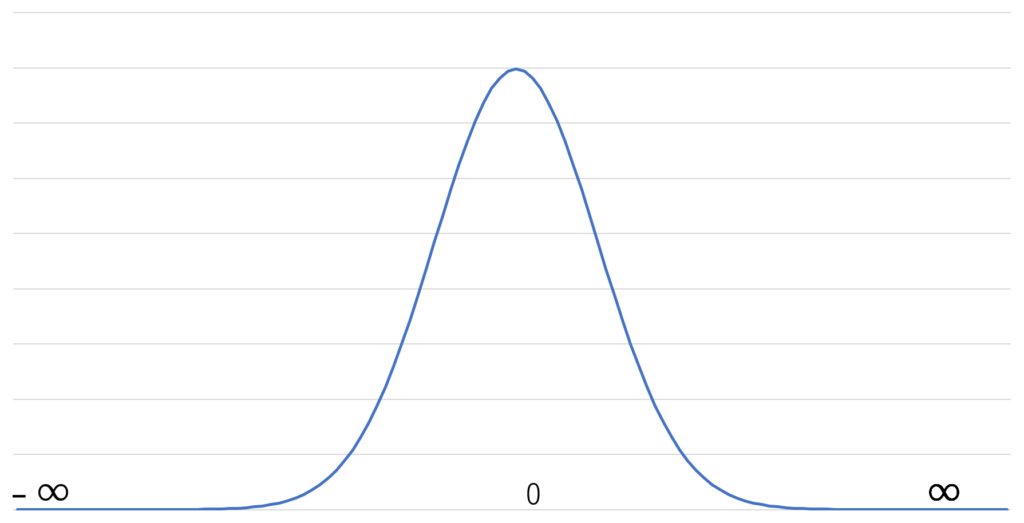

標準正規分布の性質

標準正規分布には大きく２つの特徴があります。

平均値と標準偏差を変更すると分布の形が変わる

標準正規分布は平均値が1,標準偏差が0でした。標準分布に対して平均値を2とすると分布がプラス方向に2だけ移動します。また標準偏差を2とすると分布が2倍に広がります。(若干、ペッちゃんこになる)

標準偏差の2個分以内のデータが95%を占める

今回の話のメインとなるところです。正規分布の一番の特徴といっても過言ではないところで、標準偏差の2個分以内が全データの95%を占めているのです。なお、標準偏差の1個分で約70%を占めます。

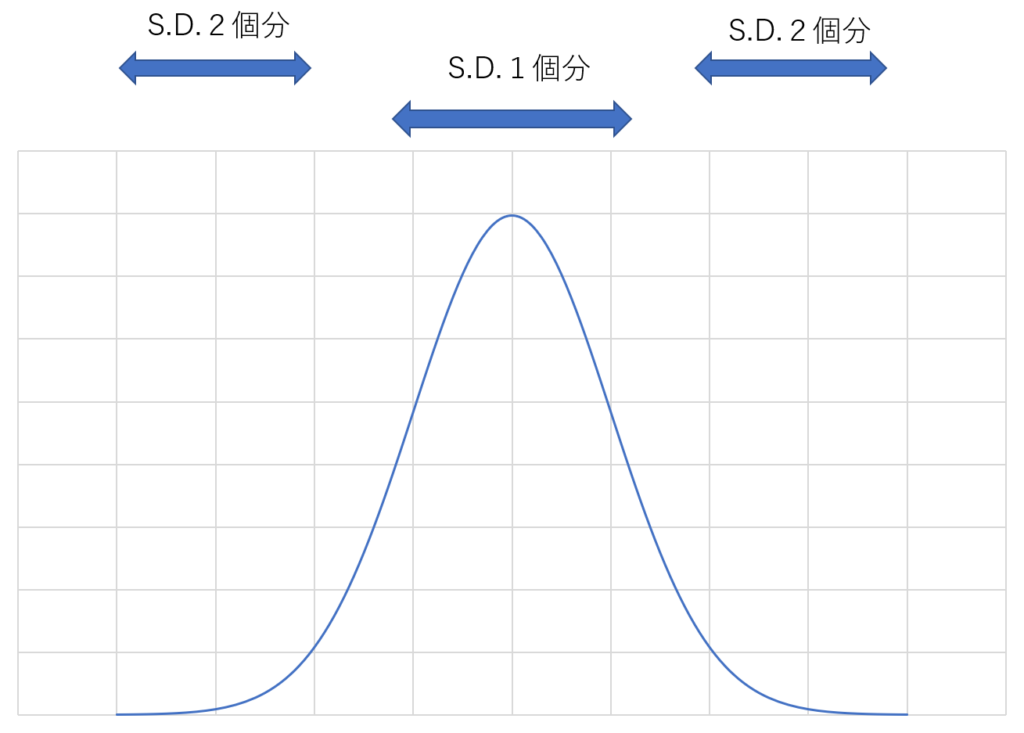つまり、95%で当たるデータが分かるのです。その95%の区間のデータ(x)を数式で表すと

となります。(数式の説明は余裕があれば追記します)

パチンコと正規分布

この正規分布をパチンコに適用した場合、どんなことがわかるのでしょうか。
パチンコは予め決まった確率を1回転ごとに当たったかはずれたかの抽選をしているだけなので、シンプルで正規分布が適応できそうです。

正規分布でねらい目の台を探せるか

例えば以下のような回転数と大当たりのパチンコ台があったとします。

大当たり確率：300分の1

 

 

 

 

 

 

 

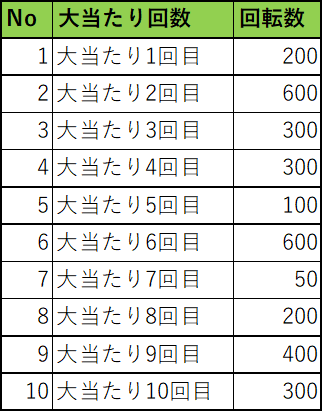
この時、平均値μは305、標準偏差は約177です。これを95%の範囲の値に当てはめると

-41～652となり、0回転以下で当選することはないことから1～652となります。すなわち以下の事が言えるでしょう

今この台が500回転まで回っていたとしたら、あと150回転以内で当たるため、ねらい目となるのではないでしょうか

正規分布ではいつ当たるか分からない

結局のところ、正規分布では95%で当たる回転数を範囲でわかりますが、ピンポイントに何回転目で当たるのかはわかりません。
上の例だと1回転目で当たる場合もあれば、652回転目でようやく当たる場合もあります。さすがに『95%の確率で652回転以内で当たるよ』と言われても300分の1なんだから2倍ハマり以内には大体あたるだろうと思ってしまいます。

もしかしたら、統計学で必勝となる解答がないので、”ギャンブル”と言われているのかもしれません。

まとめ

お薦め書籍

私もこの本に書かれている、”95パーセント予言的中区間”を参考にして、パチンコ×統計学の可能性を考えました。
数式の具体的な導き方に興味があれば是非手に取ってみてください。