標準偏差について

今回は統計学の中でもとても重要な標準偏差について紹介します。標準偏差は、「分散の正の平方根」や「データや確率変数のばらつきを表す指標」であります。一言で説明してもどういった背景があるのかなどがわからなければ、頭にすーっと入ってきませんね。したがって、本稿ではそういった面を交えながら標準偏差とは何ぞやをご紹介したいと思います。

標準偏差とは？

ここでは具体例を使って標準偏差について説明をしていきます。例は「平均の種類」で使ったテストの点数を使います。改めて下表にテストの点数を記載します。

表1 A組の国語のテストの平均点について

Aくん	60
Bくん	50
Cくん	80
Dくん	70
Eくん	40

表2 B組の国語のテストの平均点について

Fくん	60
Gくん	60
Hくん	60
Iくん	60
Jくん	60

どちらのクラスも国語の平均点は60点です。ここで、この平均点からだとどちらのクラスも同程度の実力と言えるでしょうか。もし、70点以上を取らないと合格できない大学試験があったとしたら、A組からは2人、B組からは0人となります。とても同程度とは言えそうにありませんね。

平均点とはあくまでもこの平均点の周りに多くの点数が集まるということです。そのため、平均点だけはそれぞれのクラスがどういった性質を持っているのかがわかりません。

では、どのようにすれば性質がわかるでしょうか。考えられるとしたら、それぞれの受験者が平均点とどの程度の差があるのかを見たいと思います。ここで、A組の各受験者の平均点との差は下表となります。

表3 A組の各受験者の平均点との差

Aくん	０
Bくん	-10
Cくん	+20
Dくん	+10
Eくん	-20

マイナスが平均点より小さい場合を表しており、プラスが平均点より大きい場合を表しています。この平均点との差の値のことを統計学では「偏差」と呼んでいます。

さて、次に欲しいのは平均点と同様な代表する一つの値です。それでは、偏差を全て足して割ってみてはどうか。実は足すと、「0」になってしまい、情報がなくなってしまいます。偏差の合計を取ると必ず、「0」になってしまうことが数学の世界では証明されているのです。

次の手としては「平均の種類」で紹介のあった「二乗平均」を思い出してほしいと思います。二乗平均はデータの平均値から各値を差し引いて「ばらつき」を出す平均であると説明しました。今回の行っている方法と同じです。そのため二乗平均をならって行うとすると「各値を2乗して合計をとったあと、個数で割って最後にルートをとる」ことをすればいいわけです。

計算式は以下になります。

√(0^2 + (-10)^2 + 20^2 + 10^2 +(-20)^2)/5 =√200 ≒ 14

ルートを取る前の値は200となりました。この時の単位は各値を2乗しているため「点の2乗」というよくわからない単位になっています。そのため、最後にルートを取っいるのです。このルートを取る前の値のことを統計学では「分散」と呼び、とても重要な指標となっています。

そしてルートを取ったあとの14点が「ばらつき」を表しています。この値からA組は「平均60点の前後14点くらいに点数が散らばっている」ということができます。

この値の事を統計学では「標準偏差」と呼んでいます。また、標準偏差のことを「S.D.(Standard Deviation)」ということも多いです。

標準偏差から何がわかる？

標準偏差とは、平均を基準にどれだけ値が離れているかを表す数値です。その標準偏差がわかると以下のことがわかります。

1．あるデータの集まりから、取り出したデータの性質
2．複数のデータの集まり同士を比較した性質

あるデータの集まりから、取り出したデータの性質がわかる

例えば、とあるテストの平均点が60点であるときにあなたが75点を取ったとします。この場合、あなたは優秀と言えるでしょうか。確かに平均点を15点上回っているため、優秀とも言えます。しかし、同様な人は何人いるでしょうか

ここで判断材料として出るのが標準偏差です。この話を言い換えると、あなたの偏差(15点)と同等の人はどれくらいいるかということです。

結論からいうと、このテストの標準偏差が15点だった場合、あなたは「普通」と言えます。それはクラス内でも偏差15点の人が多いからです。
また、このテストの標準偏差が7点だった場合、あなたは「優秀」と言えます。それはクラス内では偏差7点の人が多いからです。

実はこの結論は数学的に既に了承を得ている話で、「正規分布」に従っているものは上記の内容が当てはまるのです。正規分布では、標準偏差1個分に該当する割合が全体の70%になるため、標準偏差一個分は特殊なわけでもなく、「普通」と言えます。一方、標準偏差2個分は全体の5%しかなく、「特殊」であると言えるのです。

正規分布は下図の形をしています。

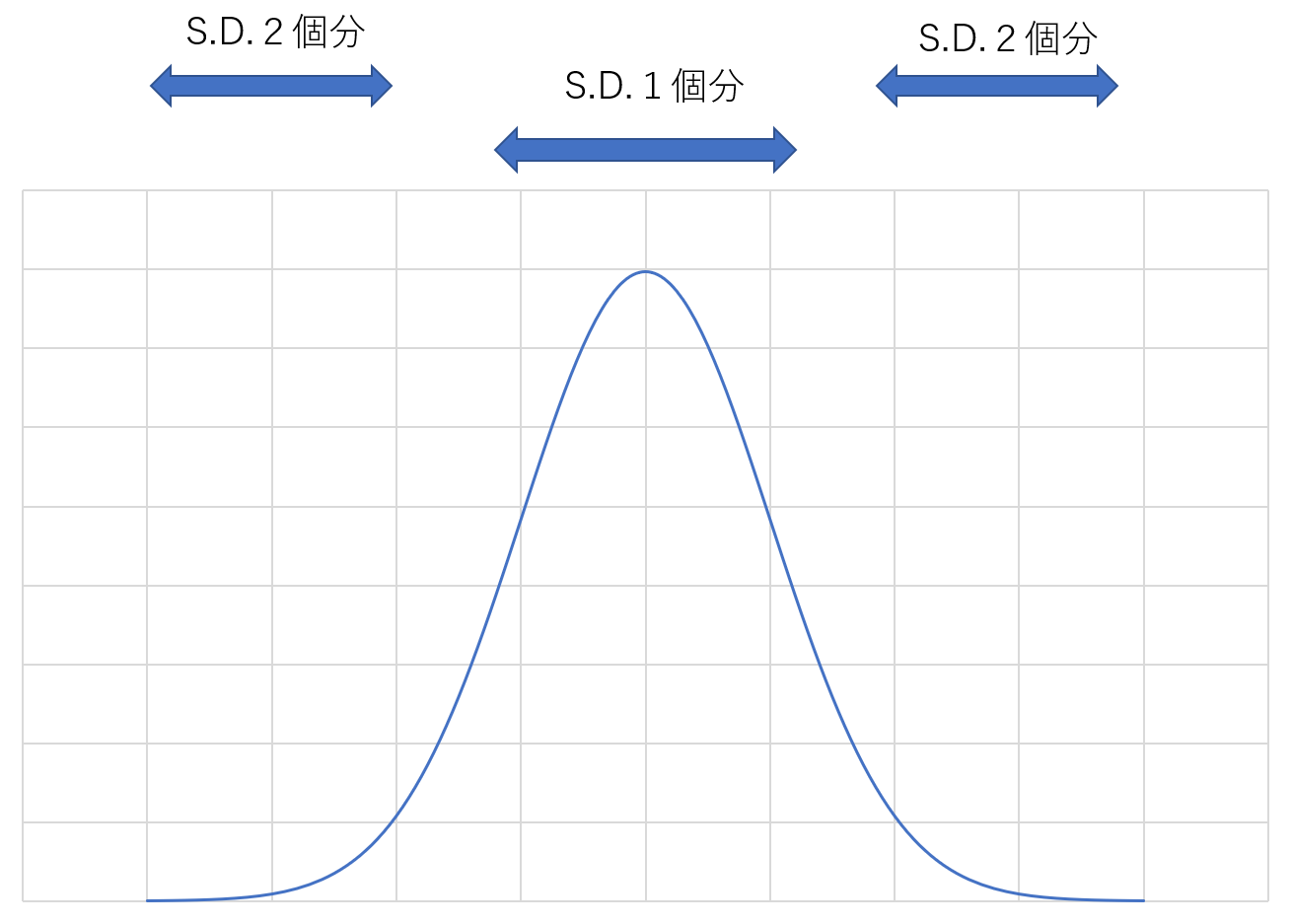
複数のデータの集まり同士を比較した性質

その他にも標準偏差がわかれば、複数のデータの集まり同士を比較して性質の違いを得ることができます。

例えば、大学受験の模試を例に説明します。下表のようなA君とB君の過去3回の模試の結果があったとします。

	A君	B君
1回目	300	450
2回目	320	200
3回目	290	100

このとき、A君の模試結果は平均が「303点」、標準偏差が「12点」です。一方のB君は平均が「250点」、標準偏差が「147点」です。両者を比較すると、A君はB君より平均点数が高いことがわかります。

ここで、模試で350点以上取れなければ合格できない大学があった場合はどうでしょうか。A君はとれても315点ですが、B君は397点とれるため、B君の方にチャンスがありそうです。

このように、標準偏差がわかれば、データの集まり同士の「ムラ」が分かるようになります。この例だと、A君はムラが少ないが、B君はムラが多いことになります。

標準偏差の活用

ここでは標準偏差を使う例として投資について紹介します。

株式では、一年通してとある銘柄の株が1カ月の間で何%値上がりまたは、値下がりしたかを表す「月次平均収益」があります。例えば以下の表の月次平均収益の銘柄があったとします。

年度	2016	2017	2018
月次平均収益	+2.04	-1.5	+0.5

2016年度を見ると平均収益が2.04%となっています。これは1年通して毎月の投資した分の2.04%利益があるということなり、毎月100万円を投資したら、120万円になるわけです。

こんなおいしい話はあるでしょうか。

これは、あくまでも1年間の平均を取っているわけであるため、毎月ごとに変動しています。各月の平均収益は下表となります。

月	平均収益
1月	-2.8
2月	9.3
3月	11.4
4月	3
5月	-7.5
6月	2.5
7月	-0.6
8月	1.8
9月	5.1
10月	-2.3
11月	-6
12月	10.6

このように月によってはマイナスになることもあり、よい月は+11.4%になるが、悪い月は、-7.5%になります。

すなわち、月次平均収益だけではよい株かどうかが決められないということです。

そこで必要となる指標が標準偏差です。

毎月の偏差から月次の標準偏差を求め、どれくらい上振れもしくは下振れするかを表します。この投資における月次の標準偏差のことを『ボラティリティ』または『予想変動率』と呼び、結局のところリスクを表す指標となっていますし、同時にチャンスの指標でもあります。あらため、先ほどの表を以下に示します。

年度	2016	2017	2018
月次平均収益	+2.04	-1.5	+0.5
ボラティリティ	5.6	2.3	1.2

つまり、月次平均収益は2.04%でも、月によっては「+7.64～－3.56」にぶれることは大いにあるということです。

まとめ

参考書籍